Optellen gehele getallen
In Van natuurlijke naar gehele getallen hebben we gezien dat de gehele getallen uiteenvallen in twee groepen: de positieve gehele getallen en de negatieve gehele getallen, waarbij 0 tot beide groepen behoort, althans in (onder meer) België en Frankrijk. De positieve gehele getallen zijn niets anders dan de natuurlijke getallen, en hoe je die bij elkaar optelt heb je in de lagere school geleerd.
Als we het optellen van natuurlijke getallen veralgemenen naar het optellen van gehele getallen, dan is het enige nieuwe dat er naast positieve (gehele) getallen, ook negatieve (gehele) getallen kunnen voorkomen. Deze veralgemening lijkt in het begin misschien moeilijk, maar is het eigenlijk niet. Het voornaamste is dat je begrijpt waar gehele getallen op neer komen, en wat het betekent dat je ze bij elkaar optelt.

Om het optellen van gehele getallen aanschouwelijk te maken, zal ik hierna gebruik maken van de Hilbert Wolkenkrabber. Zoals je in Gehele getallen op de getallenas hebt gelezen, is dit een wolkenkrabber met een oneindig aantal verdiepingen boven de grond, een oneindig aantal verdiepingen onder de grond, en een reeks liften die oneindig kunnen stijgen en oneindig kunnen dalen, maar waarvan er altijd minstens één klaarstaat op de benedenverdieping (verdieping 0).
Hiernaast zie je de Hilbert Wolkenkrabber afgebeeld. De benedenverdieping is grijs ingekleurd, de verdiepingen boven de grond groen, en de verdiepingen onder de grond rood.
Elke verdieping bevat het nummer van de verdieping. Voor de verdiepingen onder de grond gebruiken we negatieve gehele getallen, voor deze boven de grond gebruiken we positieve gehele getallen. Het positieve toestandsteken laten we weg, zoals we dat ook in echte gebouwen doen. Voorbeeld: naar de negende verdieping boven de grond verwijzen we eenvoudigweg met "9" en niet met "+9". Voor de verdiepingen onder de grond gebruiken we uiteraard wel het toestandsteken, zoals in "ik ga naar min 3" of "mijn fiets staat op min 1".
Bovenaan en onderaan zie je een halve verdieping met daarin drie puntjes. Dit is om aan te geven dat er geen hoogste en ook geen laagste verdieping is.
Als
De gehele getallen zullen we ook gebruiken om uit te drukken hoeveel verdiepingen de lift stijgt, of daalt, vertrekkend van verdieping 0.
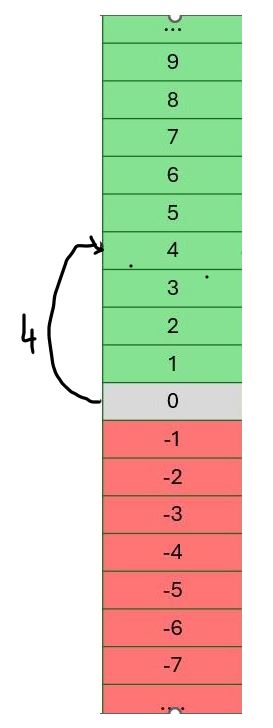
Stijgt de lift bijvoorbeeld 4 verdiepingen vanaf de benedenverdieping, zoals in de linker afbeelding hiernaast, dan zullen we het getal +4 gebruiken om naar deze verplaatsing te verwijzen.
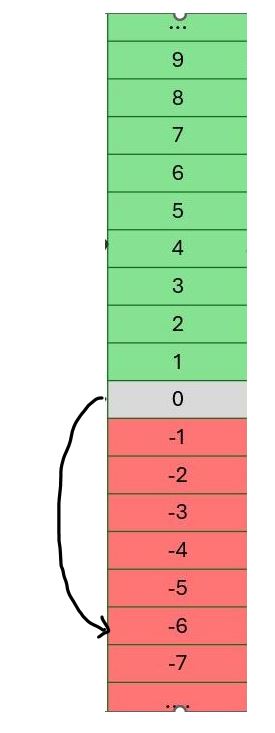
Daalt de lift 6 verdiepingen vanaf de benedenverdieping, zoals in de rechter afbeelding hiernaast, dan zullen we het getal –6 gebruiken om naar deze verplaatsing te verwijzen.
Het optellen van twee gehele getallen zullen we vergelijken met twee keer na elkaar de lift nemen in de Hilbert Wolkenkrabber. Dit kan in dezelfde richting zijn (twee keer stijgen of twee keer dalen). Het kan uiteraard ook in een verschillende richting zijn: eerst stijgen en dan dalen, of omgekeerd. We spreken wel af dat de lift de eerste keer steeds vertrekt van de benedenverdieping (verdieping 0).
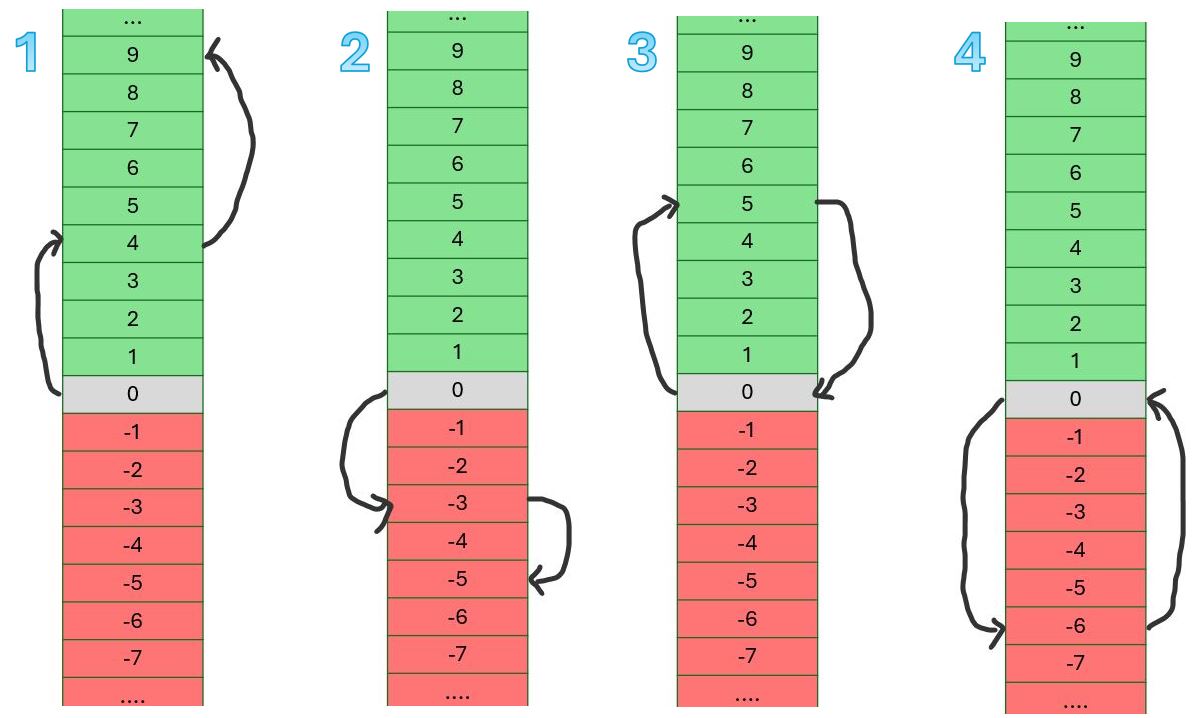
Om aan te geven hoeveel verdiepingen je stijgt of daalt zullen we pijlen gebruiken: een pijl links van de wolkenkrabber voor wat je eerst doet (bijvoorbeeld zes verdiepingen stijgen) en een pijl rechts voor wat je daarna doet (bijvoorbeeld acht verdiepingen dalen).
Hiernaast zie je vier voorbeelden. In afbeelding 1 stijgt de lift twee keer, in afbeelding 2 daalt ze twee keer. In afbeelding 3 stijgt de lift eerst om daarna te dalen. In afbeelding 4 is dat omgekeerd: eerst dalen, dan stijgen.
Om het optellen van gehele getallen te illustreren, zullen we dit alles nu vertalen naar een bewerking met gehele getallen. Hoe doen we dat?
Dat de lift twee keer na elkaar stijgt of daalt, zullen we uitdrukken met het bewerkingsteken voor de optelling, het plusteken dus.
Hoeveel verdiepingen de lift stijgt of daalt zullen we uitdrukken met een natuurlijk getal. Dus zowel voor vier verdiepingen stijgen als voor vier verdiepingen dalen zullen we het getal 4 gebruiken. (In de voorbeelden hierna zullen we het verband leggen met de absolute waarde van een geheel getal.)
Om het verschil te maken tussen stijgen en dalen zullen we het toestandsteken gebruiken. Zals je kan vermoeden zullen we het het positieve toestandsteken gebruiken om aan te geven dat de lift stijgt, en het negatieve toestandsteken om aan te geven dat de lift daalt.
Laat ons dit bekijken met een aantal concrete voorbeelden, om het wat minder abstract te maken.
Voorbeeld 1
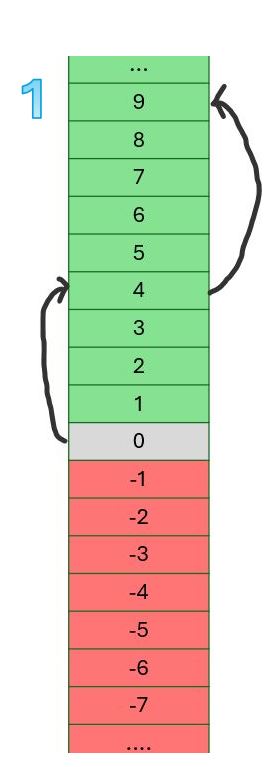
Bekijk de afbeelding rechts. De zwarte pijl links stelt voor dat je in de lift stapt op de benedenverdieping (verdieping 0) en vandaar vier verdiepingen stijgt. De zwarte pijl rechts stelt voor dat je, vanop de vierde verdieping, nog eens vijf verdiepingen stijgt, waardoor je uiteindelijk terecht komt op de negende verdieping. Hoe geven we dit nu weer in een bewerking met twee getallen?
Het bewerkingsteken van de optelling gebruiken we om uit te drukken dat we eerst het ene doen (vier verdiepingen stijgen) en daarna het andere (vijf verdiepingen stijgen). Het aantal verdiepingen dat we stijgen, drukken we uit met een natuurlijk getal. Dat we eerst vier verdiepingen stijgen, drukken we uit met het getal 4, en dat we daarna vijf verdiepingen stijgen, drukken we uit met het getal 5.
Dat het hier in beide gevallen gaat om stijgen (en niet om dalen) drukken we uit met het positieve toestandsteken. Alles samen geeft dit ons dus:
(A) (+4) + (+5)
Het blauwe plusteken in (A) staat voor het bewerkingsteken, de groene plustekens zijn toestandstekens en drukken uit dat het gaat om een aantal verdiepingen stijgen. In termen van de wolkenkrabber vergelijking, lees je de optelling (+4) + (+5) als "eerst vier verdiepingen stijgen (vanaf verdieping 0) en daarna vijf verdiepingen stijgen".
In (A) komen twee gehele getallen voor: +4 en +5. Om te bepalen wat de som is van deze twee gehele getallen, pas je de bewerkingsregel toe voor de optelling van gehele getallen. Daarvoor zet je twee stappen:
- Je bepaalt het toestandsteken voor de uitkomst.
- Je bepaalt de absolute waarde voor de uitkomst.
Laat ons deze twee stappen afzonderlijk bekijken.
Stap 1: toestandsteken van de som bepalen. Wat het toestandsteken is van de som, hangt af van de vraag of de twee getallen hetzelfde toestandsteken hebben of een verschillend toestandsteken. Hebben de getallen hetzelfde toestandsteken (wat hier het geval is), dan is het toestandsteken van de uitkomst hetzelfde als dat van de twee getallen. In (A) zal het toestandsteken voor de uitkomst dus positief zijn (+). Wat het toestandsteken wordt wanneer de twee getallen een verschillend toestandsteken hebben, bespreek ik in een later voorbeeld.
Merk op dat het logisch is dat het toestandsteken voor de som van (+4) + (+5) positief is. Wat (+4) + (+5) uitdrukt is dat de lift, vertrekkend van 0, eerst verdiepingen stijgt, en daarna nog eens vijf verdiepingen stijgt. Hierdoor kan de lift evident niet terechtkomen op een verdieping onder de grond, en moet het toestandsteken van de som dus positief zijn.
Stap 2: absolute waarde van de som bepalen. Hoe je hiervoor te werk gaat, hangt opnieuw af van de vraag of de twee getallen hetzelfde toestandsteken hebben of een verschillend. Hebben de getallen hetzelfde toestandsteken (wat hier het geval is), dan neem je de som van de absolute waarden van de twee getallen. Laat ons dit wat in meer detail bekijken voor ons voorbeeld.
De twee getallen in (+4) + (+5) hebben hetzelfde toestandsteken. Om de som te bepalen, moet je dus de absolute waarden van de twee getallen bij elkaar optellen. De absolute waarde van +4 is 4. In symbolen noteer je dit als |+4| = 4. De absolute waarde van +5 is 5. In symbolen noteer je dit als |+4| = 4. De bewerkingsregel zegt dat, aangezien de twee getallen hetzelfde toestandsteken hebben, je hun absolute waarden moet optellen om de absolute waarde van de som te bekomen. Dat betekent dat we de som moeten maken van |+4| en |+5| en dat is 9.
Combineren we nu de twee stappen, dan krijgen we:
(B) (+4) + (+5) = +9Aangezien we het positieve toestandsteken mogen weglaten, kunnen we dit ook ook noteren als:
(C) (+4) + (+5) = 9Elders heb je gezien dat we het bewerkingsteken voor de optelling mogen weglaten, om op die manier minder tekens te moeten schrijven, en dat je het positieve toestandsteken bij het begin van een opgave ook mag weglaten. We kunnen de optelling in (C) dus ook schrijven als:
(D) 4 + 5 = 9
en dat is gewoon een optelling van twee natuurlijke getallen, zoals je dat ook gezien hebt in de lagere school.
Als je (B) met (D) vergelijkt, dan zal je nu wel denken dat we alles nodeloos complex aan het maken zijn. We voeren eerst toestandstekens in, waardoor we een optelling krijgen met drie toestandstekens zoals in (B), terwijl het eigenlijk gewoon neerkomt op een optelling van twee natuurlijke getallen, zoals in (D).
Dat we zo te werk gaan, heeft een reden. Zoals je in latere voorbeelden zal helpt het expliciet maken van stijgen versus dalen door middel van positieve en negatieve toestandstekens om het optellen van gehele getallen inzichtelijk te maken.
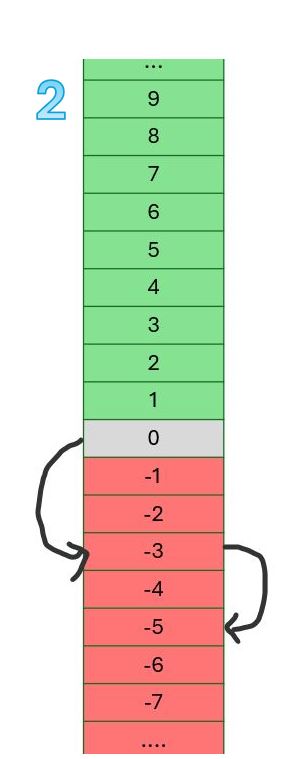
Voorbeeld 2
Ook in ons tweede voorbeeld vertrekt de lift van de benedenverdieping, maar dit keer daalt ze twee keer na elkaar. Zoals je kan zien aan de pijlen, daalt ze eerst drie verdiepingen, waardoor ze terecht komt op verdieping min 3, en daarna daalt ze nog eens twee verdiepingen, om terecht te komen op verdieping min 5.
Laat ons ook dit vertalen naar een optelling van twee gehele getallen.
Zoals in het eerste voorbeeld, gebruiken we het bewerkingsteken van de optelling om uit te drukken dat we eerst het ene doen (in dit geval drie verdiepingen dalen) en daarna het andere (twee verdiepingen dalen). Het aantal verdiepingen dat we stijgen, drukken we ook hier uit met een natuurlijk getal. Dat we eerst drie verdiepingen dalen, drukken we uit met het getal 3, en dat we daarna 2 verdiepingen dalen, drukken we uit met het getal 2.
We moeten wel duidelijk maken dat het gaat om dalen en niet om stijgen, zoals in het eerste voorbeeld. Dat drukken we uit met het negatieve toestandsteken. Voegen we het negatieve toestandsteken toe aan de natuurlijke getallen 3 en 2 uit de vorige paragraaf, dan bekomen we de gehele getallen –3 en –2. Dat zijn de getallen die we gebruiken in onze optelling om de verplaatsingen van de lift weer te geven:
(E) (–3) + (–2)
Zoals in het eerste voorbeeld, staat het blauwe plusteken in (E) voor het bewerkingsteken en zijn de twee tekens in het groen toestandstekens.
De optelling in (E) laat ons toe om het verband te leggen met de absolute waarde van een getal. Elders heb je gezien dat de absolute waarde van een geheel getal a bekomen wordt door het toestandsteken van a weg te laten. Pas dit toe op het eerste gehele getal in (E), namelijk –3. Laat je daarvan het toestandsteken weg, dan bekom je het (natuurlijke) getal 3.
Let goed op het verschil tussen beide: het gehele getal –3 drukt uit dat de lift drie verdiepingen daalt. De absolute waarde van –3 (zijnde het getal 3) drukt alleen uit hoeveel verdiepingen de lift stijgt of daalt, niet in welke richting de lift stijgt of daalt. Met de gehele getallen kan je beide uitdrukken: aantal verdiepingen én richting van de verplaatsing (naar boven of naar beneden).
In (E) komen twee gehele getallen voor: –3 en –2. Om te bepalen wat de som is van deze twee gehele getallen, pas je de bewerkingsregel toe voor de optelling van gehele getallen. Zoals we in voorbeeld 1 hebben gezien, zet je daarvoor twee stappen:
- Je bepaalt het toestandsteken voor de uitkomst.
- Je bepaalt de absolute waarde voor de uitkomst.
Laat ons ook hier deze twee stappen afzonderlijk bekijken.
Stap 1: toestandsteken van de som bepalen. Wat het toestandsteken is van de som, hangt af van de vraag of de twee getallen hetzelfde toestandsteken hebben of een verschillend toestandsteken. Hebben de getallen hetzelfde toestandsteken (wat hier het geval is), dan is het toestandsteken van de uitkomst hetzelfde als dat van de twee getallen. Voor (E) zal het toestandsteken voor de uitkomst dus negatief zijn (–).
Merk op dat het logisch is dat het toestandsteken voor de som van (–3) + (–2) negatief is. Wat (–3) + (–2) uitdrukt is dat de lift, vertrekkend van 0, eerst drie verdiepingen daalt, en daarna nog eens twee verdiepingen daalt. Hierdoor kan de lift evident niet terechtkomen op een verdieping boven de grond, en moet het toestandsteken van de som dus negatief zijn.
Stap 2: absolute waarde van de som bepalen. Hoe je hiervoor te werk gaat, hangt opnieuw af van de vraag of de twee getallen hetzelfde toestandsteken hebben of een verschillend. Hebben de getallen hetzelfde toestandsteken (wat hier het geval is), dan neem je de som van de absolute waarden van de twee getallen. Laat ons ook dit wat in meer detail bekijken voor ons voorbeeld.
De twee getallen in (–3) + (–2) hebben hetzelfde toestandsteken. Om de som te bepalen, moet je dus de absolute waarden van de twee getallen bij elkaar optellen. De absolute waarde van –3 is 3. In symbolen noteer je dit als |–3| = 3. De absolute waarde van –2 is 2. In symbolen noteer je dit als |–2| = 2. De bewerkingsregel zegt dat, aangezien de twee getallen hetzelfde toestandsteken hebben, je hun absolute waarden moet optellen om de absolute waarde van de som te bekomen. Dat betekent dat we de som moeten maken van |–3| en |–2| en dat is 5.
Combineren we nu de twee stappen, dan krijgen we:
(F) (–3) + (–2) = –5
Laat ons nu proberen om opgave (F) met minder tekens te schrijven. Zoals hierboven maken we daarbij gebruik van de algemene regel dat het bewerkingsteken van de optelling mag worden weggelaten, als de toestandstekens maar worden behouden. Dit geeft ons:
(G) –3 –2 = –5Voorbeeld 3
In voorbeelden 1 en 2 verplaatste de lift zich twee keer in dezelfde richting: twee keer stijgen in voorbeeld 1, twee keer dalen in voorbeeld 2. Dat is anders in Figuur 3 hiernaast. Zoals je kan 7 stijgt de lift eerst (zeven verdiepingen) om daarna te dalen (4 verdiepingen).
Laat ons dit ook bekijken in termen van gehele getallen. We gebruiken opnieuw het bewerkingsteken van de optelling om aan te geven dat we de twee verplaatsingen samenvoegen en we gebruiken gehele getallen voor de verplaatsingen zelf. De lift stijgt eerst, dus ons eerste getal zal een positief toestandsteken hebben. De lift daalt daarna, dus het tweede getal zal een negatief getalsteken hebben.
Dit geeft ons:
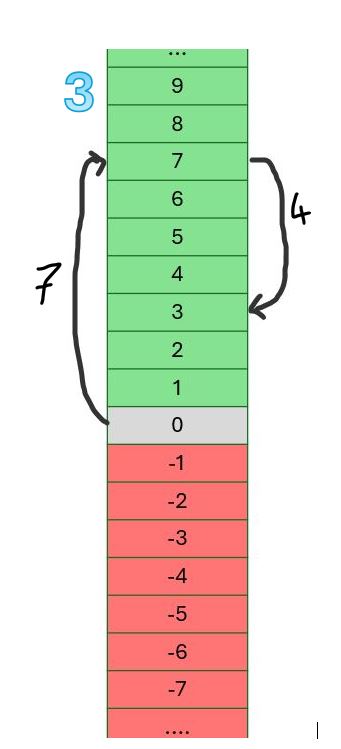
(H) (+7) + (–4)
Zoals in de twee vorige voorbeelden, zullen we ook hier de bewerkingsregel voor de optelling toepassen. Daarvoor zet je twee stappen:
- Je bepaalt het toestandsteken voor de uitkomst.
- Je bepaalt de absolute waarde voor de uitkomst.
Beide stappen zullen nu iets anders verlopen dan in de vorige voorbeelden, omdat de twee getallen een verschillend toestandsteken hebben. Laat ons dit in detail bekijken.
Stap 1: toestandsteken van de som bepalen. Wat het toestandsteken is van de som, hangt af van de vraag of de twee getallen hetzelfde toestandsteken hebben of een verschillend toestandsteken. In (H) hebben de getallen een verschillend toestandsteken. In dat geval moet je kijken naar het toestandsteken van het getal met de grootste absolute waarde. Het toestandsteken van dat getal wordt het toestandsteken van de som.
Laat ons dit toepassen op de optelling in (H). Het getal met de grootste absolute waarde is +7, want 7 is groter dan 4. Het toestandsteken van +7 is positief, dus het toestandsteken van de som zal positief zijn (+).
Merk op dat het logisch is dat het toestandsteken voor de som van (+7) + (–4) positief is. In onze wolkenkrabber vergelijking, drukt een geheel getal met een positief toestandsteken uit dat de lift zich boven de grond bevindt, een getal met een negatief toestandsteken drukt uit dat de lift zich onder de grond bevindt. Aangezien de lift Figuur 3 meer verdiepingen stijgt dan daalt, kan het niet dat de lift onder de grond zou terechtkomen. Als je, vertrekkend van de benedenverdieping, meer stijgt dan daalt, dan kom je hoe dan ook terecht op een verdieping boven de grond. En, aangezien de som uitdrukt op welke verdieping je terechtkomt, als je de twee verplaatsingen samenvoegt, moet in dit geval het toestandsteken van de som positief zijn.
Stap 2: absolute waarde van de som bepalen. Hoe je hiervoor te werk gaat, hangt opnieuw af van de vraag of de twee getallen hetzelfde toestandsteken hebben of een verschillend. In dit geval hebben de twee getallen een verschillend toestandsteken. De bewerkingsregel voor de optelling zegt dat je in zo'n geval het verschil moet berekenen van de absolute waarden van de twee gehele getallen, en daarvoor trek je de kleinste absolute waarde af van de grootste. In ons voorbeeld is 4 de kleinste absolute waarde en 7 de grootste. Je moet dus uitrekenen hoeveel 7 – 4 is. De absolute waarde van de som wordt dus 3.
Combineren we nu de twee stappen, dan krijgen we:
(H) (+7) + (–4) = +3
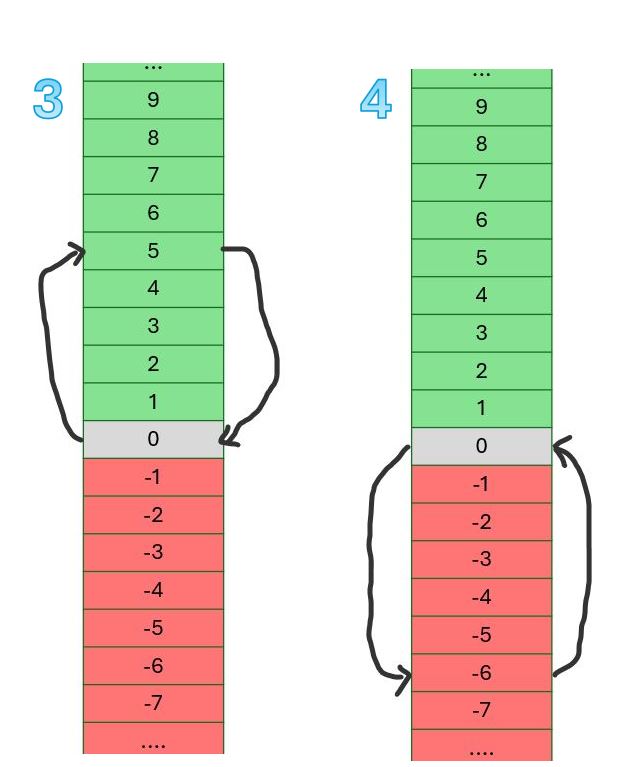
Voorbeeld X
In de twee afbeeldingen hiernaast is de begintoestand en de eindtoestand dezelfde: vertrek en aankomst op de benedenverdieping. Het enige verschil tussen beide is de volgorde van stijgen: in Figuur 3 stijgt de lift eerst om daarna te dalen, in Figuur 4 is dit omgekeerd.
Bekijk eerst Figuur 3. Het aantal verdiepingen dat de lift stijgt, en daarna daalt, is 5. Zoals tevoren drukken we het stijgen van de lift uit met het positieve toestandsteken, het dalen van de lift uit met het negatieve toestandsteken, en de opeenvolging van de twee verplaatsingen met het bewerkingsteken voor de optelling. Dit geeft ons:
(H) (+5) + (–5)
Zoals je kan zien heb je hier twee gehele getallen met een verschillend toestandsteken, maar met dezelfde absolute waarde, want |+5| = |–5| = 5. De twee getallen zijn dus tegengestelde getallen, en zoals je hebt gezien op de pagina over tegengestelde getallen, is de som van twee tegengestelde getallen steeds 0. De som van de optelling in (H) is dus 0:
(I) (+5) + (–5) = 0
Laat ons ook hier proberen om het met minder tekens te schrijven. Het bewerkingsteken van de optelling kunnen we weglaten, en ook het positieve toestandsteken als het helemaal vooraan staat. Als we dat doen, dan krijgen we:
(I) 5 –5 = 0
Zetten we dezelfde stappen voor Figuur 4, en proberen
(J) (–6) + (+6) = –6 + 6 = 0